Long-term power estimation of a Wave Energy Converter
Estimación de la producción a largo plazo de un convertidor de energíaundimotriz
A. D. de Andres, R. Guanche*, J. A. Armesto, F. del Jesus, C. Vidal, I.J. Losada
Instituto de Hidráulica Ambiental – IH Cantabria, Universidad de Cantabria,
C/ Isabel Torres 15, Parque Científico y Tecnológico de Cantabria, 39011 Santander, España
*Corresponding author: guancher@unican.es
Telephone +34 942 201 616; Fax : +34 942 266 361
Abstract
This study presents a methodology to obtain the long-term power performance of a wave energy converter on a certain location, specifically in this case a two body heave converter. The methodology is based firstly on a selection technique (MaxDiss) which selects the most representative sea states on a certain location within the occurrence matrix. After this sea state selection, the power production of the WEC is computed through the IHWave2wire model. This model was built substituting the entire Cummins equation system with a state space system, thereby avoiding the convolution integral of the radiation force. Then, based on this model the instantaneous power of the device can be obtained.
Based on a global reanalysis database (GOW from Reguero et al(2012)) the long term power series can be computed. This database accounts with climate-data for the last 60 year. Then, from the power production obtained with the numerical model and though a multidimensional interpolation technique (Radial Basis Function from Camus et al (2011a)) the whole power production lifecycle can be obtained with a good accuracy compared with the traditional method lf multiplying the power and occurrence matrix.
Resumen
Este estudio presenta una metodología para obtener la producción a largo plazo de un convertidor undimotriz en una localización determinada, en este caso se utiliza un captador undimotriz formado por dos cuerpos que absorbe la energía del oleaje en alteada. La metodología se basa en primer lugar en una técnica de selección (MaxDiss) que selecciona los estados de la mar más representativos en un cierta localización con una matriz de ocurrencia. Después de esta selección de estados de mar, la producción del WEC se calcula a través del modelo IHWave2wire. Este modelo se construyó sustituyendo todo el sistema de ecuaciones que gobierna el captador con un sistema de espacio de estados, evitando de este modo la integral de convolución correspondiente a la fuerza de la radiación. Por tanto, a través de este modelo, se obtiene la serie de potencias instantáneas del dispositivo.
Basado en una base de datos de reanálisis global (GOW de Reguero et al (2012)), se puede obtener la serie de potencia de largo plazo. Esta base de datos cuenta con datos climáticos de los últimos 60 años. Entonces, a partir de la producción de energía obtenida con el modelo numérico y mediante una técnica de interpolación multidimensional (Radial Basis Function de Camus et al (2011a)) se puede obtener todo el ciclo de vida de la producción de energía con una buena precisión comparada con el método tradicional que consiste en multiplicar la matriz de potencia y la matriz de ocurrencia.
Keywords: State-space, Time Domain Model, Wave energy converter, Long- term
Palabras clave: Espacio de estados, Modelo en el Dominio del tiempo, Captador Undimotriz, largo plazo
Index
3.-Performance optimization and long term analysis
1. Introduction
The assessment of wave energy converters is based on the power production of the studied converter on a particular location. Therefore, this assessment is based primarily on two type of inputs. On the one hand, the input regarding the climate characteristics on the study location that is shown by the occurrence matrix (percentage of occurrence of each sea state). On the other hand, the data that contents the behavior of the converter. Nowadays, the most accepted way to compute this WEC behavior is the power matrix (that represents the absorbed power per sea state).
In order to compute the annual energy power on a certain site, the classical method suggest to multiply the occurrence matrix by the power matrix. However, this method, does not take neither the shape and particularities of both matrix, nor the interannualvariability of the wave energy resource. This approximation, then, is not totally precise and then further research on this topic is needed. This paper will present a new approach in order to obtain the long term power estimation of a WEC. This approach will consist on a sea state selection technique, a time domain model and a non linear interpolation technique.
In order to obtain the power performance of a Wave Energy converter, the first step is to build a numerical model that simulates the behavior of this converter. This behavior can ba analyzed numerically using frequency, (see Henriques et al (2012) or Gomes et al (2012) or time-domain models, (see Alves (2012) being the frequency domain the most widely used due to its simplicity and low computer requirements. Frequency-domain analysis provides the fundamentals of the body motion under regular or irregular waves, but its intrinsic linear approach cannot simulate the floater\’s behavior under steep waves, large displacements or rotations and non linear forces associated to the Power Take Off (PTO), hydrodinamic drag or the mooring system, Alves (2012).
To assess the non linear behavior of Wave Energy Converters (WEC) under irregular waves, 3D CFD models can be used with a high computational cost. Another (less accurate and costly) approach is to use numerical models based on the time-domain equations of motion of the floating body Cummins(1962). In these equations, the wave forces (incident, diffracted and radiated) are solved by an external frequency-domain numerical model, while the rest of the forces can be expressed with all their non-linear characteristics. The equations solve the time movements of the body, so its relative position is taken into account.
The presence of the convolution integral in Cummins equation difficults its solution in the time domain. To avoid this problem, one of the methods proposed in the literature is to approximate the convolution integral by a state-space system Yu(1995). Taghipour etal(2008) shows that solving the convolution integral is approximately 8 times slower than using state-space realizations. The problem has moved from solving the convolution integral to finding the elements of the state-space system which approximate that convolution integral. This state-space receives as input the velocity of the body and produce an approximation to the convolution integral as output. Several approaches have been used in the literature, for example Yu(1995), Duclos(2001), Kristiansen et al(2005), McCabe et al(2005).
The state-space which approximates the convolution integral can be extended to a new state-space that completely replaces Cummins equation Yu(1995), Alves(2012). The new state-space receives as input the excitation force and produces as output the movement of the body.
The present work uses a model based on Taghipour et al (2008), Perez et al(2011) to identify the state-space which approximates the convolution integral. This model uses a Boundary Element Method to compute the added mass and damping coefficients for a given set of frequencies, and then the transfer functions associated to these frequencies is computed. The coefficients of the state-space system are calculated using an identification method in the frequency domain, Perez et al(2009) which meets the requirements given in Perez(2011). Finally the state-space is extended to solve Cummins equation Yu(1995), Alves (2012).This model is then used to analyze the behavior of the two-body WEC floating in heave presented Babarit et al(2012).
Then in this paper firstly, the numerical model is presented and secondly a methodology in order to obtain the long term performance of a wave energy converter is presented.
2.-Numerical Model
The WEC geometry to be analyzed in this paper, corresponds to a two-body point absorber consisting of two objects: a buoy (1), that is only partially submerged and a float (2) that floats on the top of the surface. Both objects are only allowed to move in heave and the union between the bodies is made via a linear PTO connection.
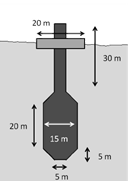
Figure 1: Two body heaving converter analyzed
The Cummins equations for a two-body heave converter are given by Eqn (1) and (2):
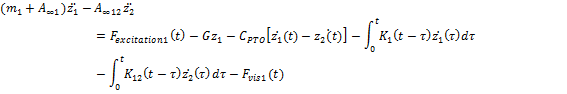 (1)
(1)
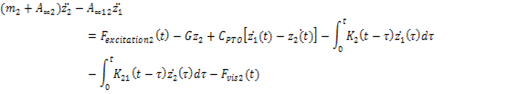 (2)
(2)
where:
- mi is the mass of the object considered
- A∞ is the infinite added mass of the object considered (at infinite frequency)
- zi (t) is the vertical displacement of the body (z origin at the Still Body Level, SBL) and the dots mean the order of partial time derivation
- Fexcitation is the excitation force
- G is hydrostatic stiffness of the object considered
- CPTO is the PTO linear damping coefficient
- ∫Ki(t-t)zi(t)dt represents the convolution integral where K(t) represents the fluid memory effect function(or impulse response function)
- Fvis represents the viscous effects drag force
The most challenging task in Cummins equations is to efficiently solve the convolution integral. This integral is not convenient for the analysis of motion of WEC systems. In order to avoid this problem, a method proposed in the literature is to approximate the convolution integral by a state-space system, Yu(1995). Doing so the problem becomes finding the elements of the state-space system which approximates the convolution integrals. This state-spaces receives as input the velocity of the body and produces an approximation to the convolution integral as output. Several approaches have been used in the literature, for example Yu(1995),Duclos et al(2001), Kristiansen(2005).A description of the different methods can be found in Taghipour et al (2008). These techniques share a starting point, as all of them require the use of information taken from a 3D Boundary Element Method (BEM) such as WAMIT/WADAM.
Each convolution integral in Eqn. (1) and (2) is approximated by a state-space:
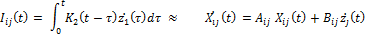
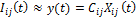 (3)
(3)
i = 1,2, j = 1,2 where Xij(t) is the state-space vector and zj(t) is the input of the system.
Following Taghipour et al (2008) once the coefficients for the state space system previously mentioned are obtained using WADAM and the identification technique Perez et al (2009) a global state-space is built and the free dynamics of the 2 body WEC can be described by a global state-space representation. Using this global state-space approach, the whole Cummins equation can be replaced by the state-space equations that are expressed as (4).
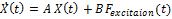
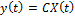 (4)
(4)
Where in (4) the input of the state-space is the excitation force, Fexcitation(t) the output is the state-space vector X(t) that comprises the four state-space vectors of the convolutions, the displacement and the velocity vectors.
The results of this system are the displacements and velocity of the two body WEC through the time. Then, from these results the power output of the WEC can be computed. Further explanation of this method is found in de Andres et al (2013). Also, in this paper the model has been validated thorugh a comparison with a the solution of WADAM. The validation is shown in figure 2.
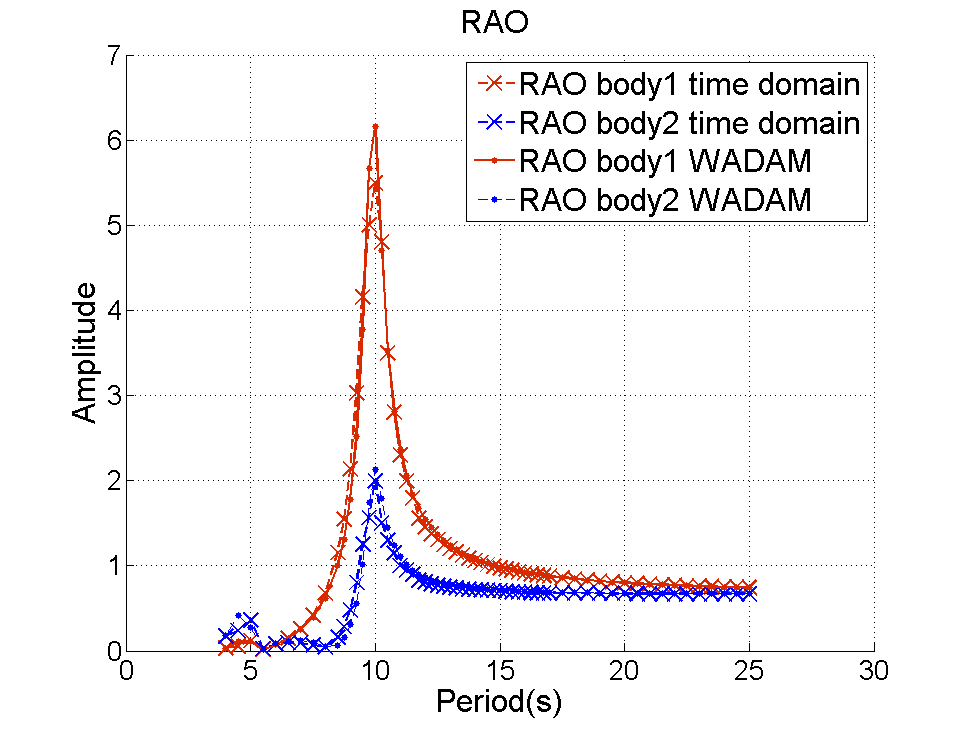
Figure 2:Validation of the model
3.-Performance optimization and long term analysis
The objective of this section is to carry out the optimization of the PTO constant for the selected wave climate in order to maximize the energy production.
Heave converters usually comprise one the following PTOs:
- Direct linear generators
- Hydraulic piston-accumulator-hydraulic motor-generator
- Rack and pinion – gearbox – generator
Whatever the PTO selection it is possible to regulate the damping constant (usually through the generator excitation) in order to maximize the wave energy absorption for each sea state. This PTO control can be carried out in two ways 1) setting a fixed optimum value of CPTO for each sea state or 2) instantaneously modifying the CPTO in terms of the incoming waves and the heave motion. This second option will improve the energy production but it implies the instantaneous measurement of the incoming waves and WEC heave motion and a fast response of the control system. In the approach proposed here, option 1 has been chosen, and a new methodology is proposed to select the optimal for every single sea state.
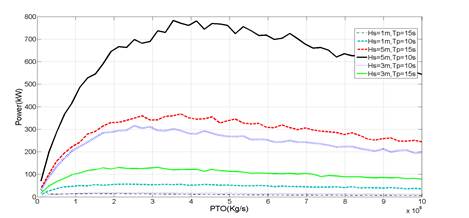
Figure 3: PTO Constant optimization
To fulfill that objective, the numerical model described in section 2 was run for a selected range of irregular sea states with wave heights and peak periods comprising the Hm0-Tp scatter diagram shown in Figure 5. For each sea state, a hundred of PTO constants from 105 to 107 Kg/s were tested. Figure 3 shows one example of the energy production in terms of the PTO constants for several sea states. As can be seen in this figure, for each sea state there is a optimum value of the CPTO in terms of energy production. Once this optimal CPTO is obtained, the optimal power matrix can be built (see figure 4 ).
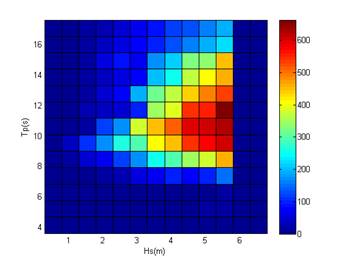
Figure 4: Power matrix of the device (kW)
The yearly averaged optimal energy production of the heave device in a given wave climate is usually obtained by multiplying the optimized power matrix by the Hm0-Tp scatter diagram. If a sea state time series is available at a given location, the sea state time series of optimal energy production can be obtained interpolating each time series sea states on the optimal power matrix.
The previous approach has two main sources of inefficiency:
1) many of the sea states computed to build the optimal power matrix are useless because their probability is zero and
2) if a linear interpolation is used to compute the time series of sea states of optimal power, the changes in the slope on the production matrix are not taken into account.
To avoid these inefficiencies, a new methodology to calculate the sea states time series of optimal energy production is proposed below. This methodology is applied to a node of the 60-year reanalysis data base, Global Ocean Waves (GOW) from Reguero et al(2012) located near Santoña (North Spain) made up of hourly sea states.
The first source of inefficiency is addressed using a selection technique to separate a subset of sea states from the data base that best represent all the data base sea states. In this methodology, the MaxDiss algorithm from Snarey et al (1997) is proposed because it represents very well the boundaries of the data base in a multidimensional domain. It is based on a selection that computes the distance between points in a multidimensional space and selects the most distant points it order to cover the whole variability of the set. For the second inefficiency source, the Radial Basis Function (RBF) interpolation method from Franke et al (1982) is used. This methodology has been used previously in Camus et al (2011) to study the downscaling of wave climate to coastal areas. This methodology has been proved as one of the best interpolation methodologies for multidimensional data.
In order to check the goodness of the method and the optimal size of the selected subset of sea states, a year-long time series of sea states (year 2001, 8737 sea states) of energy production has been computed numerically, first considering all the sea states (8737) and considering the proposed methodology using different sizes(from 50 to 3500) of the MaxDiss subset of sea states.
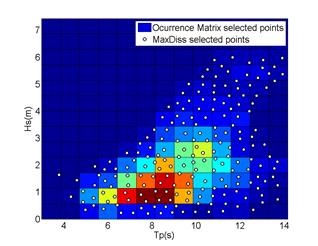
Figure 5: MaxDiss technique, selected sea states
The complexity of the MaxDiss+RBF methodology is justified here in terms of precision with respect to the traditional method of multiplying the frequency and power matrices. To compare the accuracy of the proposed methodology with the traditional one, the 2001 year series was reconstructed also by interpolating each time series sea states on the 14×14=196 sea states of the power matrix using the RBF technique, using the proposed methodology with a MaxDiss subset of sea states with the same size as the power matrix (196 cases) and rebuilding the full year time series using the RBF technique (see figure 5).
The correlation coefficients between the true time series of the power production (numerically simulated sea state by sea state) and the reconstructed ones was 0.96 for the proposed methodology and 0.7 for the one using the power matrix and the RBF interpolation technique. In Table 1, the yearly averaged energy production is computed using:
1) the time series of sea states energy production obtained by computing all 8737 sea states,
2) the product of power and frequency matrices, (196 sea states computed)
3) the time series of sea states energy production reconstructed using the power matrix and RBF (196 cases computed) and
4) the proposed MaxDiss+RBF methodology computing 196 cases.
| Method | Number of executed cases | Mean Annual Power | % of error |
| 8737 Sea state Run | 8737 | 274 kW | 0 % |
| Power matrix*Occurence matrix | 196 | 148 kW | -46 % |
| Selection of equally distributed sea states+ RBF | 196 | 190 kW | -31 % |
| MaxDiss+ RBF | 196 | 245 kW | -11 % |
Table 1: Methods tested
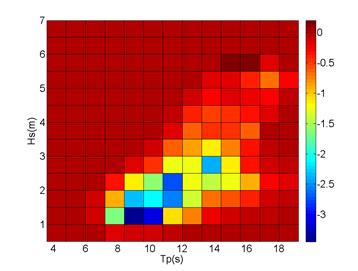
Figure 6: Percentage of relative error between method 2 and exact method
As can be noticed, the percentage difference between each method and the exact (full time domain computation) are 46 % for method 2, 31% for method 3 and 11% for the proposed methodology. Figure 6 shows the contribution of each sea state of the (scatter diagram) to the relative error on the yearly averaged energy production computed using method 2. The maximum error is located around the 10 s peak period, where the power matrix has a local ridge and the (scatter diagram) nears it maximum and the concavity of the power production matrix provides the interpolation of each sea state energy production always below the true one. Therefore, this methodology provides a good approach in terms of computational effort that understimates the power production in a minor way than the traditional methodology. A smaller cell size and then a greater computational effort, from the traditional method in order to gain achieve the same accuracy.
Finally, figure 5 shows the MaxDiss selected subset of sea states: it has to be highlighted that most of the sea states are concentrated on the Hm0-Tp region where sea states are probable (192 points on the 90 % probability volume) while using the equally-spaced power matrix, only 121 points are in the same volume.
Taking into account that the proposed methodology only computes 2% of the sea states of the data set, it is clear the advantage of the new methodology. Also the inaccuracy of the traditional methodologies used to compute the yearly-mean of energy power production to rebuild the full time series have been demonstrated.
If the range of the sea state variables Hm0-Te does not change, neither does the number of sea states on the MaxDiss subset. For example, the full 60-year hourly sea states time series of energy production can be rebuilt with similar accuracy computing the energy production of only 200 sea states with the numerical model. Figure 7 represents the yearly mean and the standard deviation of the 60 year rebuilt time series using 200 and 1000 subset of sea states in the MaxDiss selection. Moreover there is no noticeable difference between the two curves. The average power produced by the device is 300 kW, being the worst year in terms of production 1962 with 260 kW and the best year 1960 with 340 kW. Therefore, with the methodology presented in this paper the most important statistics of the life cycle of a wave converter can be obtained in a reliable way.
Finally, in order to clarify and summarize all the quantities related to power production Table 2 is presented:
| Nominal Power | 1 MW |
| Average Power | 300 kW |
| Capacity factor | 30 % |
| Mean annual production | 2602 MWh/year |
Table 2: Key figures
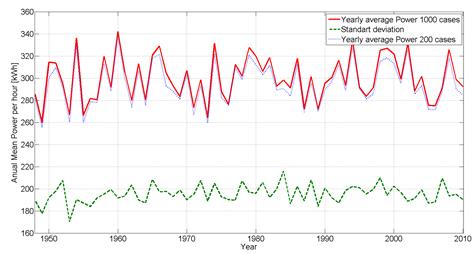
Figure 7: 60-year power production series
Conclusions
In this paper, a new methodology to estimate the long-term power performance of a wave energy converter has been proposed and validated. This methodology apart from computing the annual energy power with more accuracy than the traditional method of multiplying the scatter plot and the power matrix, estimates the long term variability of the power production.
This new methodology relies on a sea state selection technique (MaxDiss). This technique selects the most relevant sea states in aoccurrence matrix. These selected sea states are used to obtain the power production of a particular WEC with a time domain model.
This time domain model has been built with the frequency-domain identification of Perez and Fossen and the state-space transformation of Yu and Falnes. This model has been used to check the behavior of a two-body heaving WEC. After validation of the time-domain model using the WADAM frequency-domain numerical code, the WEC performance in a given wave climate has been optimized assuming that the PTO\’s damping is optimal in terms of energy absorption and constant during each sea state.
The developed numerical model has shown to be accurate and efficient in terms of computer time and provides a good tool to analyze the response of a WEC and also has the advantage to allow the implementation of non linear forces (i.e. drag or PTO forces) or complex control methodologies based on the actual position or velocity of the WEC.
In order to obtain the long term power series, after computing the absorbed power by the wave energy converter a non-linear interpolation technique was used. Using the RBF function and from the climate data extracted from the GOW database the whole power series can be computed.
This method was checked with the traditional one and some variations and has been found to be computationally efficient and very useful in order to compute the interannual variability of power production. Also, the underestimation of the mean annual power by the traditional method (- 46%) is improved by the proposed methodology (-11%).
Bibliography
[1] Babarit, A., Hals, J., Muliawan, M., Kurniawan, A., Moan, T., and Krokstad, J., 2012. “Numerical benchmarking study of a selection of wave energy converters”. Renewable Energy, 41, pp. 44 – 63.
[2] Yu, Z., and Falnes, J., 1995. “State-space modelling of a vertical cylinder in heave”. Applied Ocean Research, 17(5), pp. 265 – 275.
[3] Taghipour, R., Perez, T., and Moan, T., 2008. “Hybrid frequency-time domain models for dynamic response analysis of marine structures”. Ocean Engineering, 35(7), pp. 685 – 705.
[4] Snarey, M., Terrett, N. K., Willett, P., and Wilton, D. J., 1997. “Comparison of algorithms for dissimilarity-based compound selection”. Journal of Molecular Graphics and Modelling, 15(6), pp. 372 – 385.
[5] Henriques, J., Lopes, M., Gomes, R., Gato, L., and Falcao, A., 2012. “On the annual wave energy absorption by twobody heavingwecs with latching control”. Renewable Energy, 45, pp. 31 – 40.
[6] Gomes, R., Henriques, J., Gato, L., and Falc˜ao, A., 2012. “Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion”. Renewable
Energy, 44, pp. 328 – 339.
[7] Alves, M., 2012. “Numerical simulation of the dynamics of point absorber wave energy converters using frequency and time domain approaches.”. PhD thesis, Universidade T´ecnica de Lisboa, February.
[8] Cummins, W. E., 1962. “The impulse response function and ship motions”. Schiffstechnik, 9, pp. 101 – 109.
[9] Kashiwagi, M., Endo, K., and Yamaguchi, H., 2005. “Wave drift forces and moments on two ships arranged side by side in waves”. Ocean Engineering, 32, pp. 529–555.
[10] Perez, T., and Fossen, T. I., 2011. “Practical aspects of frequency-domain identification of dynamic models of marine structures from hydrodynamic data”. Ocean Engineering,
38, pp. 426 – 435.
[11] Perez, T., and Fossen, T. I., 2009. “A Matlab Toolbox for Parametric Identification of Radiation-Force Models of Ships and Offshore Structures”. Modeling, Identification
and Control, 30(1), pp. 1–15.
[12] Camus, P., Mendez, F. J., and Medina, R., 2011a. “A hybrid efficient method to downscale wave climate to coastal areas”. Coastal Engineering, 58(9), pp. 851 – 862.
[13] Duclos, G., Clement, A. H., and Chatry, G., 2001. “Absorption of outgoing waves in a numerical wave tank using a self-adaptive boundary condition”. International Journal of Offshore and Polar Engineering, 11(3), pp. 168–175.
[14] Kristiansen, E., Hjulstad, A° ., and Egeland, O., 2005. “State-space representation of radiation forces in time domain vessel models”. Ocean Engineering, 32(1718), pp. 2195 – 2216.
[15] de Andres, A., Guanche, R., Armesto, J., del Jesus, F., Vidal, C., and Losada, I., 2013. “Time domain model for a two body heave converter: model and applications”. Ocean Engineering.
[16] Reguero, B., Menéndez, M., Méndez, F., Minguez, R., and Losada, I., 2012. “A global ocean wave (gow) calibrated reanalysis from 1948 onwards”. Coastal Engineering, 65, pp. 38 – 55.
[17] Franke, R., 1982. “Scattered data interpolation: Tests of some method”. Mathematics of Computation, 38(157), pp. pp. 181–200.
[18] McCabe, A.,Bradshaw,A.,Widden,M.,2005.A time-domain model of a floating body using transforms.In:Proceedings of the Sixth European Wave and Tidal Energy Conference University of Strathclyde, Glasgow.


.gif)